Defining an Ellipse


To define an ellipse as the current arc, use GpiSetArcParams where the values (p,s) and (r,q) are the world coordinates of the end points of the major and minor axes of the ellipse. For example, current arc parameters of (18,0) and (0,10) define an ellipse with a major axis of 36 coordinate units and a minor axis of 20 coordinate units. The resultant ellipse is shown in the following figure.

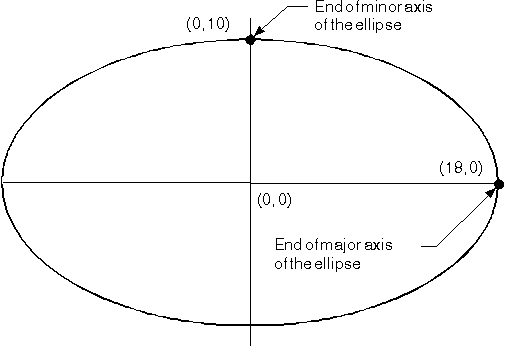
The Ellipse

For maximum accuracy, create the axes of an ellipse so that they are at right-angles to each other. You can check this by ensuring that the following equation is always true:

p x r + s x q = 0

So, to check the above example:

0 x 18 + 10 x 0 = 0

You also can define a tilted ellipse as the current arc. None of the current arc parameters for a tilted ellipse will be 0, though you should still ensure that the axes of the ellipse are at right-angles to each other. The following figure shows a tilted ellipse defined with current arc parameters of (8,6) and (-3,4).

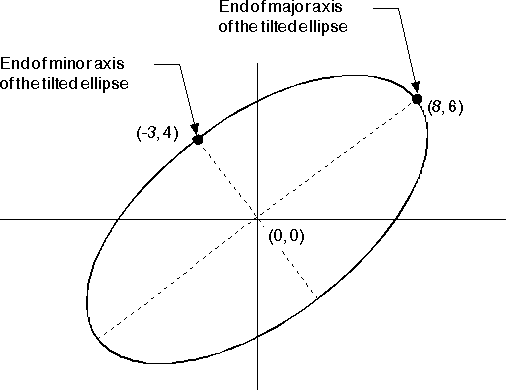
Tilted Ellipse

[Back: Full Arcs]
[Next: Defining a Circle]